• Главная
• Уроки:
  • Урок 1
  • Урок 2
  • Урок 3
  • Урок 4
  • Урок 5
  • Урок 6
  • Урок 7
  • Урок 8
  • Урок 9

Урок №8.
ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННОЙ ТАБЛИЦЫ ДЛЯ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Цель работы:

• научиться использовать электронные таблицы для выбора оптимального решения поставленной задачи и проверки правиль­ности построения математической модели.

Электронная таблица выполняет не только функцию автома­тизации вычислений. Она является очень эффективным средством проведения численного моделирования ситуации или объекта, для математического описания которых (т.е. построения математичес­кой модели) используется ряд параметров. Часть этих парамет­ров известна, а часть рассчитывается по формулам. Меняя во все­возможных сочетаниях значения исходных параметров, вы буде­те наблюдать за изменением расчетных параметров и анализиро­вать получаемые результаты. Excel производит такие расчеты быстро и без ошибок, предоставляя в считанные минуты множе­ство вариантов решения поставленной задачи, на основании ко­торых вы выберите наиболее приемлемое. Поиск решения и мо­делирование - одни из самых мощных инструментов Excel.
В данной работе рассматриваются две задачи.

ЗАДАЧА № 1

Чему будет равна численность населения России в начале третьего тысячелетия?
Сразу ясно, что задачу не решить, если не знать, как со време­нем будет меняться численность населения России, т.е. необходи­мо иметь функцию, выражающую зависимость численности на­селения от времени. Обозначим эту функцию f(t). Но такая функ­ция неизвестна, так как народонаселение зависит от многих факторов: экологии, состояния медицинского обслуживания, морали, права и даже от политической обстановки. Но, общие демогра­фические данные, можно указать общий вид функции f(t).
f(t) = a*eb-1.           (1)

где коэффициенты а, b для каждого государства свои; е - основание натурального логарифма.
Эта формула лишь приближенно отражает реальность. Одна­ко слишком большая точность и не нужна. Будет хорошо, если численность населения будет спрогнозирована с точностью до нескольких миллионов.
Как же определить а и b ? Идея состоит в том, что хотя а и b не известны, значение функции f(t) можно получить из ста­тистического справочника. Зная эти данные, можно прибли­женно подобрать а и b так, чтобы теоретические значения f(t), вычисленные по формуле (1), не сильно отличались от дан­ных справочника (т.е. максимальное отклонение теоретичес­ких результатов от фактических данных не должно быть слиш­ком большим). Каждое из отклонений - это модуль разности двух чисел: фактического и соответствующего теоретического значе­ний f(t). Максимальное отклонение называют погрешностью. Не­обходимо найти такие а и b, чтобы погрешность была наимень­шей.
Итак, математическая модель процесса изменения численно­сти населения такова. Предполагается, что:
I) зависимость численности населения от времени выражает­ся формулой      f(t) = a*eb-1.
2a =const и b=const,  следует считать справедливым лишь для не очень большого промежутка времени (например, 40 лет);
3)значения а и b можно найти с достаточной точностью, ми­нимизировав погрешность.
Исходные данные: сведения из статистического справочника за период с 1960 по 1995 г. (60<=t<=95).

Результаты:

1)значения а и b.
2) численность населения России в 2000 г. (при t=100).
Кроме того, установлена связь между исходными данными и результатами: сначала надо найти а и b, минимизируя погреш­ность, а затем при этих a и b вычислить значения f(100).
Итак, математическая модель составлена. Использование элек­тронной таблицы освобождает нас от составления программы. Нужно только определенным образом записать в таблицу исход­ные данные и математические соотношения, входящие в модель. После этого можно начать процесс численного моделирования исследуемой ситуации, т.е. подбор коэффициентов а и b в форму­ле (1), а затем определение численности населения.

ХОД РАБОТЫ

ЗАДАНИЕ 1.  Заполните таблицу.

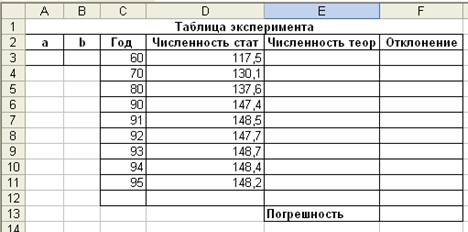
1.1. Сделайте заголовок и заполните шапку таблицы.
1.2. Столбцы А и В отведите под коэффициенты а и b соответ­ственно.
1.3. В столбец С занесите значения t с 1960 г.
1.4. В столбец D занесите взятые из справочника значения чис­ленности населения России с I960 г.

ЗАДАНИЕ 2. Подберите значения коэффициентов а и b.
Следующий шаг в решении задачи - это вычисление теорети­ческой численности по формуле (1), в которой не известны значе­ния коэффициентов а и b. Подбор а и b можно произвести в два этапа. Сначала определим их значения приближенно, для чего построим график роста статистической численности и аппрокси­мируем его. Затем уточним полученные коэффициенты а и  b с использованием функции Excel Поиск решения.
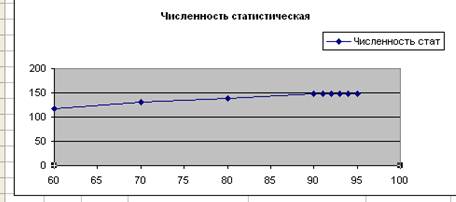
2.1.Постройте график типа X-Y по данным таблицы. (Х-годы; Y- статистическая численность).
2.2. Перемасштабируйте оси Х и Y.
Для более наглядного представления данных необходимо перемасштабировать оси.

• Выделите ось X.
• Вызовите контекстно-зависимое меню и выполните коман­ду: Формат оси -  Шкала
• Установите минимальное значение X, основную единицу измерения  и пересечение с осью У.
• Аналогично Перемасштабируйте ось Y.

2.3. Аппроксимируйте полученную кривую.

Необходимо статистические данные по численности населе­ния представить на графике плавной кривой (аппроксимировать). Эта кривая называется линией тренда. Для построения линии тренда:

• Выделите линию графика.
• Выполните команду меню Диаграмма Добавить линию  тренда или анало­гичную команду контекстно-зависимого меню.

Откроется диалог Линия тренда.

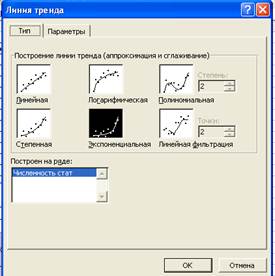
• Выберите экспоненциальный тип (см. формулу (1)).
• Выберите в диалоге Линия тренда вкладку Параметры.
• Установите флажок (*) Показывать уравнение на диаграмме и нажмите кнопку ОК.

В результате на графике появится линия тренда и уравнение с подобранными коэффициентами а и b.

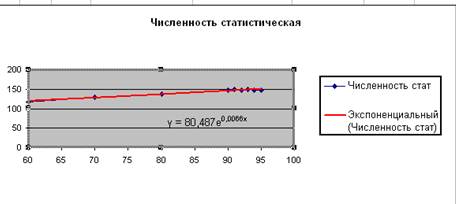
2.4. Занесите полученные значения коэффициентов а и b в ячейки A3  ВЗ и присвойте им имена:
A3 имя а
ВЗ имя b

            Коэффициенты а и b не изменяются с течением времени, это константы, следовательно, при вычислении теоретической численности они должны быть адресованы абсолютно.

ЗАДАНИЕ 3. Вычислите теоретическую численность по формуле(1).
3.1. В ячейку ЕЗ занесите формулу =а *ЕХР(b * СЗ)
3.2.Скопируйте формулу в ячейки Е4:Е11

ЗАДАНИЕ 4. Вычислите отклонение.

Отклонение - это модуль разности теоретических и факти­ческих значений функции f(t)..
4.1. В ячейку F3 занесите формулу =ABS(E3- D3)
4.2. Скопируйте формулу в ячейки F4:F11

ЗАДАНИЕ 5. Вычислите погрешность.

Погрешность - это максимальное отклонение.
В ячейку F:13 введите функцию определения максимального из чисел этого столбца.

ЗАДАНИЕ 6. Подберите значения коэффициентов а и b более точно.

При полученных в результате аппроксимации коэффициентах а и b погрешность уже неплохая (по условию она должна быть в пределах нескольких миллионов). Но коэффициенты а и b можно подобрать более тонко, используя функцию Excel Поиск решения. В отличие от Подбора параметра Поиск решения может для дости­жения нужного результата изменять или подбирать подходящие значения во многих ячейках.

6.1. Выполните команду: Сервис - Поиск решения
Если этого пункта в меню нет, то его следует загрузить, вы­полнив команду меню Сервис – Настройки.. В открывшемся диалоговом окне  следует поставить флажок (*)  около дополнения Поиск ре­шения.

6.2. Сделайте необходимые настройки в окне диалога Поиск решения

В поле  Установить целевую ячейку укажите адрес ячейки $F$13 (в ней погрешность).

• Установите переключатель(*) минимальному  значению
• В поле  Изменяя ячейки укажите $А$3:$В$3

В этом поле задаются адреса ячеек, значения которые, будут варьироваться в процессе поиска решения. В нашем случае - это адреса ячеек со значениями a и b.

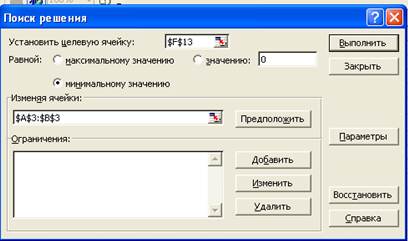
• Нажните на кнопку <Выполнить>.

            Начнется поиск решения. Так как у нас довольно точные коэффициенты а и b, то поиск займет немного времени. Когда Excel найдет решение, то откроется диалог, представленный на рисунке.

Поиск свелся к текущему решению. Все ограничения выполнены.

• Нажмите на кнопку <ОК>.

  Произойдет изменение значений ячеек в соответствии с най­денным решением. Обратите внимание, что коэффициенты а и b изменились, а погрешность уменьшилась.

ЗАДАНИЕ 7. Определите численность населения России в 2000 г.
7.1. Подставьте в ячейку С12 число 100, что соответствует 2000 г.
7.2. В Е12 скопируйте формулу из Е11.  В ячейке Е12 появится искомое число.

ЗАДАНИЕ 8.Построите на одной диаграмме совмещенные графи­ки роста численности населения на основе статистических  и  теоре­тических данных.
8.1.Выделите на построенном графике линию тренда и уда­лите ее, выполнив команду  Очистить контекстно-зависимого меню линии тренда.
8.2. Добавьте в уже построенную диаграмму теоретические данные.

• В таблице эксперимента выделите теоретические данные Е2.Е12.
• Установите указатель мыши на правой границе выделен­ного блока.
• Нажмите левую кнопку мыши и прибуксируйте  данные на диаграмму.
• В появившемся окне сделайте настройку (если это необхо­димо).

8.3.Оформите диаграмму в соответствии с рисунком, где показан примерный вид графиков.

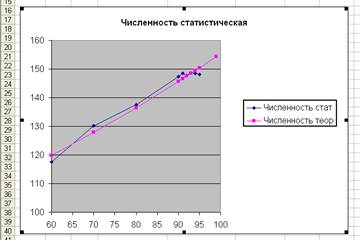
ЗАДАНИЕ 9. Оформите таблицу на свой вкус (обрамление, запол­нение, шрифты).
ЗАДАНИЕ 10. Воспользуйтесь предварительным просмотром печати.
10.1. Разместите диаграмму на одном листе с таблицей.
10.2.Добейтесь хорошего расположения таблицы и диаг­раммы на листе.
10.3. Снимите сетку.
10 4.Установите верхний колонтитул: Численное моделиро­вание. Работу выполнил <Фамилия и имя>. В нижнем ко­лонтитуле укажите дату и время.

ЗАДАНИЕ 11. Сохраните файл в личном каталоге под именем work 8_1. xls

ЗАДАНИЕ 12. Распечатайте результаты работы на принтере.

ЗАДАНИЕ 13. Проанализировав данные таблицы и графика, сде­лайте вывод об адекватности предложенной математической мо­дели реальному процессу (т.е. вывод о правильности описания рос­та населения формулой (1)).

ЗАДАНИЕ 14 (дополнительное).
Самостоятельно попробуйте выбрать для построения линии тренда другие типы, а соответственно и другие формулы для опи­сания математической модели.

Предъявите преподавателю:

• файл work8_l.xls;
• распечатку результатов работы.

ЗАДАЧА № 2

  Несколько человек решили организовать видеокафе на 6 столиков по 4 места за каждым. С каждого посетителя будет взиматься плата за сеанс видеофильма и ужин (всем посетителям будет предлагаться один и тот же набор блюд). Администрация города постановила, что плата за вход не должна превышать 5 $. Требуется определить такую входную плату, при которой будет получена наибольшая выручка.
Казалось бы, здесь и решать нечего. Разве не ясно, что чем больше входная плата, тем больше выручка. Вот и ответ: входная плата должна быть 5 $. Очень часто планирующие органы подоб­ным образом и поступают. В нашем случае если сильно увели­чить входную плату, то люди перестанут посещать кафе.
Начать надо, как всегда, с построения математической мо­дели. В чем были причины нашей неудачи? Мы предположи­ли, что посещаемость не зависит от входной платы, и получи­ли модель задачи, не соответствующую действительности. Зна­чит, надо предполагать, что посещаемость зависит от входной платы.
Обозначим входную плату через X. Тогда среднее число посе­тителей видеосалона является функцией от Х. Обозначим эту функцию через Р(Х). В задаче требуется найти такое значение А,  при котором выручка, равная произведению входной платы на количе­ство посетителей X* Р(Х), достигает максимума. Если бы функ­ция Р(Х) была известна, то найти требуемый максимум не соста­вило бы особого труда. Но эта функция не известна, поэтому попробуем найти хотя бы общий вид функции. Его можно ука­зать, обобщив опыт работы подобных кафе:

Р(Х) = ах2-bх + с.       (2)      

Коэффициенты a, b и с для каждого кафе свои. Как же их оп­ределить? Проще всего найти значение с. Представьте себе невообразимое - в видеокафе пускают бесплатно (т. е. Х=0). Ясно, что свободных мест не будет. Следовательно, P(0) равно числу мест в кафе. С другой стороны, подставив 0 вместо X, получим Р(0)=с. Значит, с равно количеству мест. В нашем случае с=24 (6 столи­ков по 4 места за каждым).
Определить а и b так же просто не удается. Справочников по посещаемости видеокафе еще нет. Поэтому здесь требуется экс­перимент.
Достаточно открыть кафе и установить на некоторый срок (дней на десять) определенную плату за вход. Среднее число посетителей и даст нам (приближенное!) значение функции. Установив другую плату за вход, найдем приближенное зна­чение Р(Х) при новом X, и так несколько раз.
Зависимость посещаемости от входной платы (на основе экспериментальных данных для конкретного кафе):

  Пользуясь электронной таблицей, можно подобрать значения а и b способом, аналогичным описанному при решении задачи № 1,т.е. минимизацией погрешности между экспериментальной и теоретической выручкой. Затем можно определить, при какой входной плате выручка будет наибольшей.

ХОД РАБОТЫ:
 ЗАДАНИЕ 1. Внимательно ознакомьтесь с постановкой задачи.
На каких предположениях строится математическая модель? Что является исходными данными? Что должно явиться результатом?

ЗАДАНИЕ 2. Заполните таблицу эксперимента.

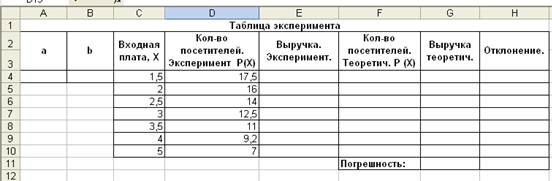
2.1. Сделайте заголовок и заполните шапку таблицы.
2.2.Отведите столбцы А и В таблицы соответственно лад коэффициенты а и b.
2.3. В столбец С занесите данные по входной плате.
2.4.В столбец D занесите экспериментальные данные по среднему числу посетителей.
2.5. В столбце Е подсчитайте выручку на основе эксперимен­тальных данных как произведение входной платы на количе­ство посетителей.

ЗАДАНИЕ 3. Подберите приближенное значение коэффициентов а и b.

            Подбор коэффициентов а и b выполняется аппроксимацией экспериментальных данных по аналогии с задачей 1.

3.1. Постройте диаграмму типа X-Y по экспериментальным дан­ным.
(X - входная плата, Y- экспериментальные данные по коли­честву посетителей).=
3.2. Аппроксимируйте полученную кривую. При построении линии тренда следует выбрать полиномиаль­ный тип (см. формулу (2)) и указать Y-пересечение = 24.

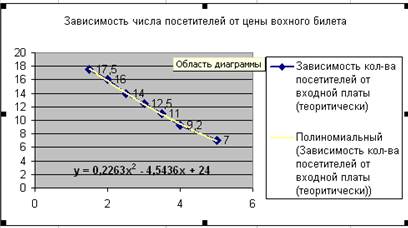
3.3. Занесите полученные значения коэффициентов а и b в таблицу.

ЗАДАНИЕ 4. Вычислите теоретическое количество посетителей и   теоретическую выручку.
4.1. В столбце F вычислите по формуле (2) теоретическое ко­личество посетителей, причем, как объяснялось выше, С=24.
4.2. В столбце G вычислите теоретическую выручку.

ЗАДАНИЕ 5. Вычислите отклонение между экспериментальной и теоретической выручкой и погрешность.
5.1.В столбце Н вычислите отклонение между эксперименталь­ной и теоретической выручкой (аналогично заданию 4 в задаче 1).
5.2. В свободной ячейке столбца Н определите погрешность
(аналогично заданию 5 в задаче 1).

ЗАДАНИЕ 6. Подберите коэффициенты а и b, стараясь минимизи­ровать погрешность (аналогично заданию 5 в задаче 1).

ЗАДАНИЕ 7. Постройте графики.
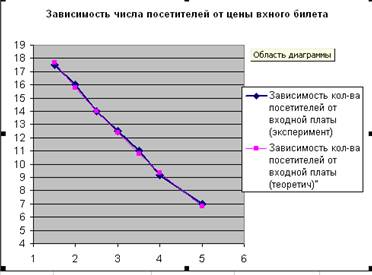
7.1.Постройте на одной диаграмме два графика типа Х-Y (экспериментальный и теоретический) зависимости коли­чества посетителей от входной платы P(Х) (аналогично за­данию 8 в задаче 1).
7.2. Разместите диаграмму на одном листе с таблицей и офор­мите, как показано на рисунке.
7.3.Постройте на одной диаграмме два графика типа X-Y (экс­периментальный и теоретический) зависимости выручки от входной платы X.

7.4. Разместите диаграмму на том же листе и оформите, как показано на рисунке.

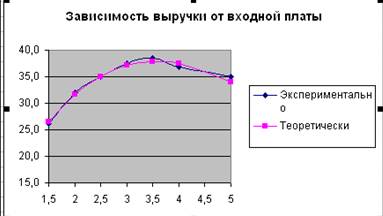
ЗАДАНИЕ 8. Определите, при какой входной плате выручка будет максимальна.
Каково среднее число посетителей сеанса при найденной опти­мальной входной плате?

ЗАДАНИЕ 9. Оформите таблицу на свой вкус (обрамление, за­полнение, шрифты).

ЗАДАНИЕ 10. Воспользуйтесь предварительным просмотром печати.
10.1. Добейтесь хорошего расположения таблицы и двух диаг­рамм на листе.
10.2. Снимите сетку.
10.3.Установите верхний колонтитул: Численное моделирова­ние. Работу выполнил <Фамилия и имя>. В нижнем колонти­туле укажите дату и время.

ЗАДАНИЕ 11.Сохраните файл в личном каталоге под именем work8_2.xls

ЗАДАНИЕ12.  Распечатайте результат работы на принтере.

ЗАДАНИЕ 13. Проанализировав данные таблицы эксперимента и график, сделайте выводы об адекватности предложенной математической модели.

ЗАДАНИЕ 14.(дополнительное) Самостоятельно попробуйте выбрать для построения линии тренда другие типы, а соответственно и другие формулы для описания математической модели.